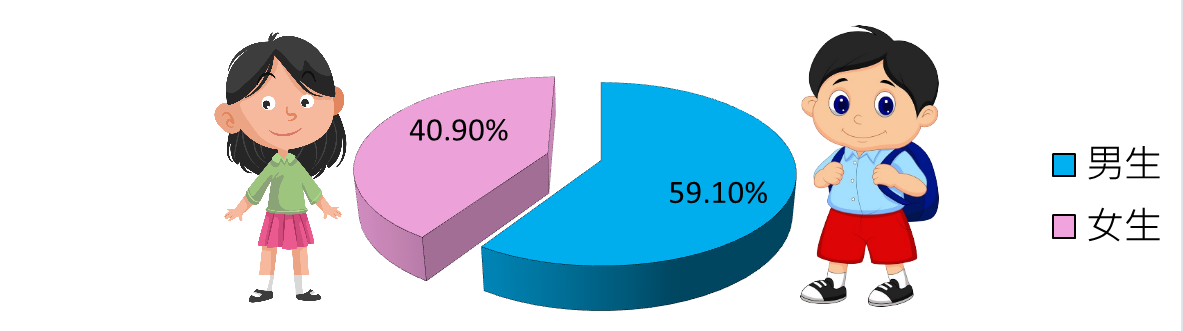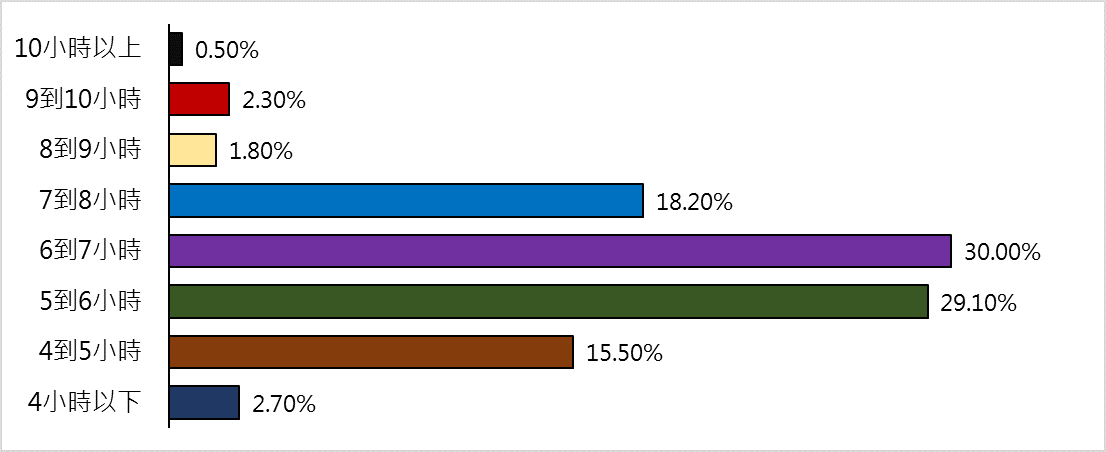弱勢助學圓夢計畫

109年經濟不利學生分析報告

為了瞭解本校圓夢生的困擾因素，採用問卷調查共計220個樣本，困擾共分為六大項，分別是課業因素、家庭因素、感情因素、經濟因素、升學就業因素與身材外貌因素，同學可以複選。

敘述統計部分:

表01.受調查的圓夢生性別

性別	人數	百分比
男生	130	59.1%
女生	90	40.9%

圖02.圓夢生男女比例圖

表02.受調查的圓夢生本學期的學雜費經費來源

經費來源

人數

百分比

由父母或親戚支付

77

35.0%

自行支付(存款或打工收入)

51

23.2%

助學減免

50

22.7%

助學貸款

42

19.1%

總計

220

100%

圖02.圓夢生本學期的學雜費經費來源圖

若以睡眠標準為7小時的標準，輕微睡眠不足的學生佔30.0%，嚴重睡眠不足的比例高達47.3%，見表03與圖03。

表03.受調查的圓夢生平均每日的睡眠時間

平均每日的睡眠時間

人數

百分比

4小時以下

6

2.7%

4到5小時

34

15.5%

5到6小時

64

29.1%

6到7小時

66

30.0%

7到8小時

40

18.2%

8到9小時

4

1.8%

9到10小時

5

2.3%

10小時以上

1

0.5%

圖03.圓夢生睡眠時間分配圖

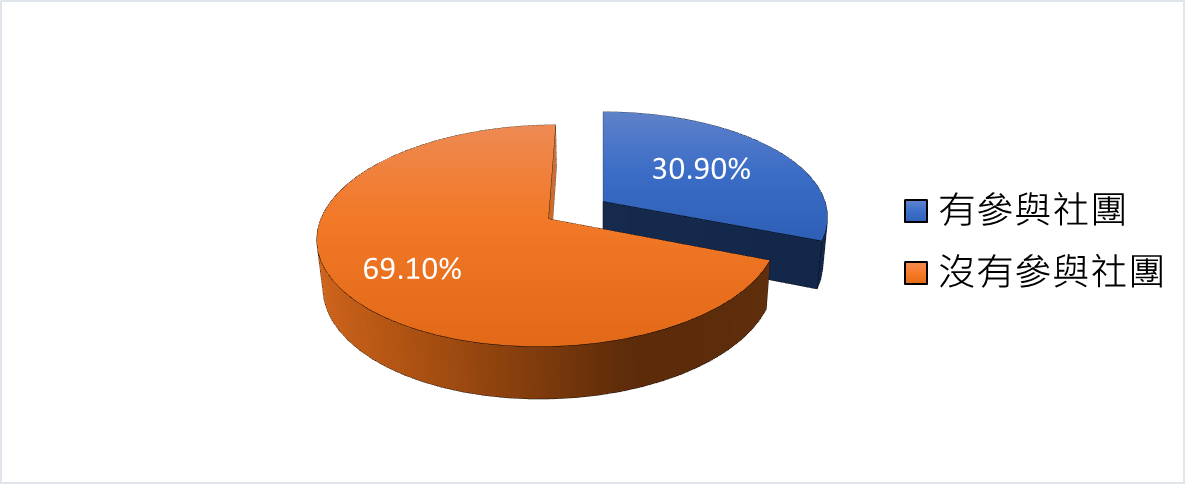
表04.受調查的圓夢生參與社團狀況

參與社團	人數	百分比
有參與	68	30.9%
沒有參與	152	69.1%

圖04.圓夢生參與社團圖

根據黃雅容(2008)的研究，第一代大學生，即父母沒有受過大學教育的大學生，很早就獲得美國學術界和政府機構的關注，在台灣則較少受到注意，研究報告指出台灣第一代大學生的背景相較於其他學生，第一代大學生女性、中低收入戶的比例較高，父親是外省人的比例較低；他們就讀技職體系和私立學校的比例較高，入學前的學業成就較低；在選校和選系時，他們比較重視經濟因素、學校地理位置因素、務實因素，對朋友同學的建議重視程度較高；他們重視的人生目標和其他學生不同，未來規劃要再念國內外研究所的比例較低。這些背景和特質基本上與美國第一代大學生相似。

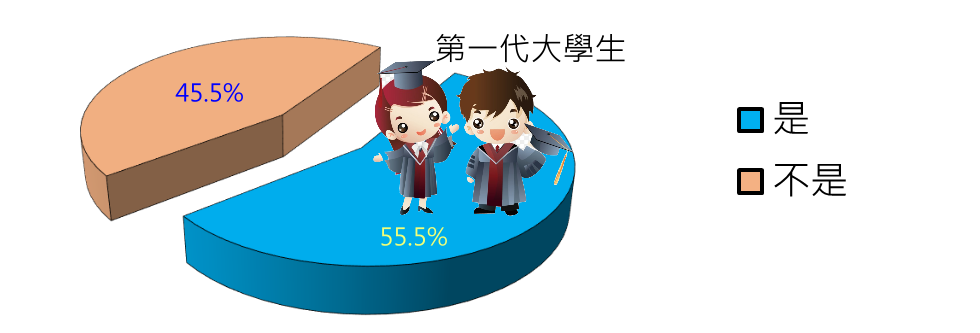
表05.受調查的圓夢生是否為第一代大學生

第一代大學生	人數	百分比
是	122	55.5%
不是	98	44.5%

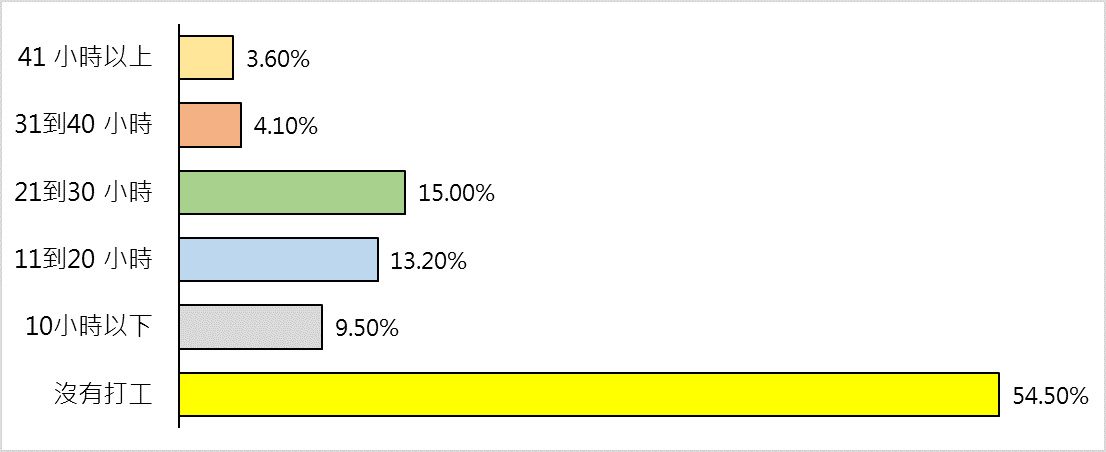
圖05. 圓夢生是否為第一代大學生圖

表06.受調查的圓夢生每週平均的打工時數

打工狀況

人數

百分比

沒有打工

120

54.5%

10小時以下

21

9.5%

11到20 小時

29

13.2%

21到30 小時

33

15.0%

31到40 小時

9

4.1%

41 小時以上

8

3.6%

圖06.圓夢生每週平均的打工時數圖

表07.圓夢的困擾

困擾	次數	百分比	觀察百分比
課業因素	101	22.4%	47.6%
家庭因素	69	15.3%	32.5%
感情因素	18	4.0%	8.5%
經濟因素	143	31.8%	67.5%
升學就業因素	82	18.2%	38.7%
身材外貌因素	37	8.2%	17.5%
總計	450	100%	212.3%

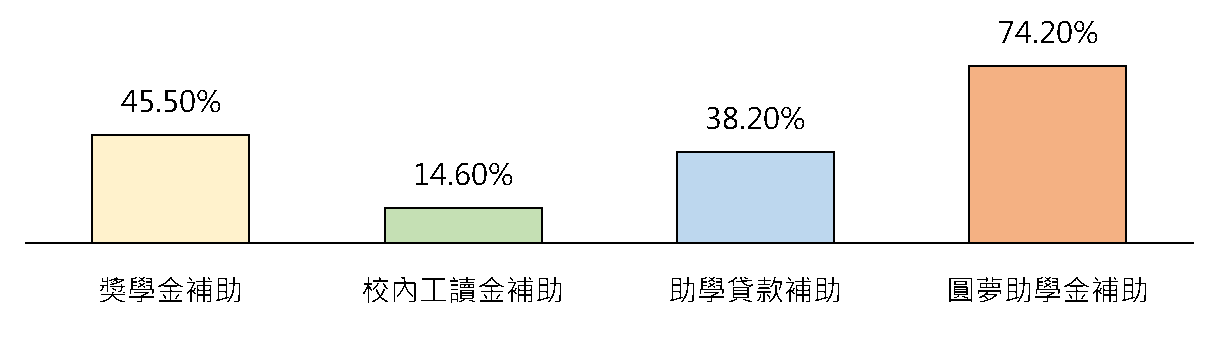
依據表07，圓夢生的困擾因素，主要原因在經濟因素(67.5%)與課業因素（47.6%）。其次為：升學就業因素（38.7%）與家庭因素（32.5%），困擾項目共勾選了450次，也就是平均每位學生平均有2.12項困擾。

表08.本學期獲得的補助

	次數	百分比	觀察百分比
獎學金補助	81	26.4%	45.5%
校內工讀金補助	26	8.5%	14.6%
助學貸款補助	68	22.1%	38.2%
圓夢助學金補助	132	43.0%	74.2%
總計	450	100%	212.3%

推論統計部分:

￭第一代大學生多為女生的推論統計

針對黃雅容2008年的研究，當時發現第一代大學生女生比例顯著較男生高，經過12年後，這種現象是否已經改變?我們以交叉表以雙母體樣本比例的比較進行分析，首先建立交叉表如下

表A.第一代大學生*性別交叉表

		性別		總計
		男生	女生	總計
第一代大學生	是	75	47	122
	不是	55	43	98
	總計	130	90	220

$$第一代女大學生比例 \; \hat p_1=\frac{47}{90}=0.52$$

$$第一代男大學生比例 \; \hat p_2=\frac{75}{130}=0.57$$

建立虛無假設與對立假設如下\[\begin{array}{l}
{H_0}:{p_1} = {p_2} \\
{H_1}:{p_1} \ne {p_2} \\
\end{array}\]

表B.卡方檢定

	數值	自由度	漸近顯著性 (雙尾)
Pearson卡方	0.644	1	0.422
連續性校正	0.442	1	.0506
概似比	0.644	1	0.422

觀察卡方值為0.644，顯著性大於0.05，結論不顯著，也可以利用

\[Z = \sqrt {{\chi ^{\rm{2}}}} \]

\[Z = \sqrt {0.644} = 0.8025 < 1.96\]

結論:經過時代的改變，第一代大學生比例已經不復過去女高於男的現象，至於省籍或入學前的學習成就不在本研究的的範圍。

￭圓夢學生綜合困擾與睡眠

表C.大學生困擾*睡眠狀況交叉表

	睡眠狀況		總數
	睡眠不足	睡眠充足	總數
課業因素	79	22	101
家庭因素	53	15	68
感情因素	16	2	18
經濟因素	110	33	143
升學就業	62	20	82
身材外貌	33	4	37
未填	5	3	8
總數	170	49	211

表D.大學生困擾與睡眠狀況數量表

　睡眠狀況個數平均數標準差

困擾數睡眠不足 170 2.08 1.264

睡眠充足 49 1.96 1.290

首先建立虛無假設與對立假設

\[\begin{array}{l}
{H_0}:{\mu _1} = {\mu _2} \\
{H_1}:{\mu _1} \ne {\mu _2} \\
\end{array}\]

先進行F 檢定，若接受兩族群變異數相等，則統計量使用

\[t = \frac{{({{\overline x }_1} - {{\overline x }_2}) - ({\mu _1} - {\mu _2})}}{{{S_p}\sqrt {\frac{1}{{{n_1}}} + \frac{1}{{{n_2}}}} }}\]

where

\[\;{S_p} = \sqrt {\frac{{({n_1} - 1)s_1^2 + ({n_2} - 1)s_2^2}}{{{n_1} + {n_2} - 2}}} \]

若F 檢定結論不接受兩族群變異數相等，則統計量使用

\[t = \frac{{({{\overline x }_1} - {{\overline x }_2}) - ({\mu _1} - {\mu _2})}}{{\sqrt {\frac{s_1^2}{{{n_1}}} + \frac{s_2^2}{{{n_2}}}} }}\]

自由度

\[{\rm{d}}{\rm{.f}} = \frac{{{{\left( {\frac{{s_1^2}}{{{n_1}}} + \frac{{s_2^2}}{{{n_2}}}} \right)}^2}}}{{\frac{{{{\left( {\frac{{s_1^2}}{{{n_1}}}} \right)}^2}}}{{{n_1} - 1}} + \frac{{{{\left( {\frac{{s_2^2}}{{{n_2}}}} \right)}^2}}}{{{n_2} - 1}}}}\]

表F.獨立樣本t 檢定

變異數相等的Levene 檢定			平均數相等的t 檢定
	F 檢定	顯著性	t	自由度	顯著性
假設變異數相等	0.378	0.539	0.570	217	0.570
不假設變異數相等	0.378	0.539	0.563	76.561	0.575

結論:雖然睡眠不足族群平均每人勾選了2.08種困擾，睡眠充足族群平均每人勾選了1.96種困擾，但差距未達顯著。

$Cohen's$效果量(Effect Size)的計算:

\[d=\frac{\bar{x_1}-\bar{x_2}}{s_p}\]

\[\;{S_p} = \sqrt {\frac{{({n_1} - 1)s_1^2 + ({n_2} - 1)s_2^2}}{{{n_1}+{n_2} - 2}}}\]

先計算$\;{S_p} = \sqrt {\frac{{(169)1.264^2 + (48)1.290^2}}{{170 + 49 - 2}}} =2.990$ 再求 $Cohen's\; d$

\[Cohen's\! \;d=\frac{2.08-1.96}{2.990}=0.04\]

說明睡眠狀況對於困擾的綜合數量影響微乎其微

￭打工對於圓夢學生課業困擾的影響

表G.圓夢學生課業困擾*打工狀況交叉表

		打工狀況		總數
		沒有打工	有打工	總數
課業因素	沒有困擾	56	63	119
	沒有困擾	46.7%	63.0%	54.1%
	有困擾	64	37	101
	有困擾	53.3%	37.0%	45.9%
	總數	120	100	220
	總數	100.0%	100.0%	100.0%

沒有打工而有課業困擾的樣本比例 $\hat{p_1}=\frac{64}{120}=0.533 $

有打工且有課業困擾的樣本比例 $\hat{p_2}=\frac{37}{100}=0.370 $

建立虛無假設與對立假設$\begin{array}{l}
{H_0}:{p_1} = {p_2} \\
{H_1}:{p_1} \ne {p_2} \\
\end{array}$進行${\rm{2}} \times {\rm{2}}$的卡方檢定

表H.卡方檢定

	數值	自由度	漸近顯著性 (雙尾)
Pearson ${\chi ^2}$	5.860	1	0.015*
Yate's連續性校正	5.221	1	0.022*
概似比	5.898	1	0.015

觀察卡方值為5.860，顯著性低於0.05，結論顯著，也可以利用

$Z = \sqrt {{\chi ^{\rm{2}}}} $的性質

\[Z = \sqrt {5.860} = 2.420^* > 1.96\]

結論:在課業的困擾上，沒有打工的圓夢生困擾的比例53.3%，打工的圓夢生困擾的比例37.0%反而較低，兩者差異達到顯著，學生為了打工賺錢，忽視學業的狀況很嚴重。

$Cohen's$效果量(Effect Size)的計算:

計算效果量前先計算 $\phi=\sin^{-1}(\hat{p})$

\[\phi_1=2\sin^{-1}(\hat{p_1})=2\sin^{-1}(0.533)=1.64\]

$\phi_2=2\sin^{-1}(\hat{p_2})=2\sin^{-1}(0.370)=1.31$

$Cohen's\;h$=$\phi_1-\phi_1=1.64-1.31=0.33$

在實驗效果量的判斷上，若其值小於0.2表示實際顯著性為低，介於0.2至0.5 表示實際顯著性為低至中等，而0.5至0.8表示實際顯著性為中至高等，高於0.8表示具有相當大的實際顯著差異(李旻憲、張俊彥，2004），此處兩者比例差異達到顯著，實際影響效果量為中等，也就是說打工對於課業的困擾上影響效果量為中等。

￭打工對於圓夢學生經濟困擾的影響

表I.圓夢學生經濟困擾*打工狀況交叉表

		打工狀況		總數
		沒有打工	有打工	總數
經濟因素	沒有困擾	45	32	77
	沒有困擾	37.5%	32.0%	35.0%
	有困擾	75	68	143
	有困擾	62.5%	68.0%	65.0%
	總數	120	100	220
	總數	100.0%	100.0%	100.0%

表J.卡方檢定

	數值	自由度	漸近顯著性 (雙尾)
Pearson ${\chi ^2}$	0.725	1	0.394
連續性校正	0.504	1	0.478
概似比	0.727	1	0.394

觀察卡方值為0.725，顯著性0.394遠大於0.05，結論不顯著，也可以利用

\[Z = \sqrt {{\chi ^{\rm{2}}}} \]

\[Z = \sqrt {0.394} = 0.627< 1.96\]

結論:在經濟的困擾上，沒有打工的圓夢生困擾的比例62.5%，打工的圓夢生困擾的比例68.0%更高，但兩者差異並未達到統計上的顯著，可以確認的是不管有沒有打工，經濟的困擾都是很高的。

$Cohen's$效果量(Effect Size)的計算:

效果量$\phi=\sin^{-1}(\hat{p})$

$\phi_1=2\sin^{-1}(\hat{p_1})=2\sin^{-1}(0.680)=1.94$

$\phi_2=2\sin^{-1}(\hat{p_2})=2\sin^{-1}(0.625)=1.82$

$Cohen's\;h$ = $\phi_1-\phi_1=1.94-1.82=0.12$

兩者比例差異沒有達到顯著，且實際影響效果量很低只有0.12，也就是說打工對於經濟的困擾上沒有什麼影響效果。

￭打工與使用3C產品對於圓夢學生睡眠的相關性影響

假設$y$ 表示圓夢生每日平均睡眠的時數

假設$x_1$ 表示圓夢生每週平均打工的時數

假設$x_2$ 表示圓夢生每日使用3C的時數

以$x_1$ 與 $x_2$ 為自變數，$y$ 為應變數進行複迴歸

設睡眠時間=常數+${\beta _{\rm{1}}}$平均打工的時數+${\beta _{\rm{2}}}$使用3C的時數

檢定 $\begin{array}{l}
{H_0}:{\beta _1} = 0\;v.s.\;{\rm{ }}{H_1}:{\beta _1} \ne 0 \\
{H_0}:{\beta _2} = 0\;v.s.\;{\rm{ }}{H_1}:{\beta _2} \ne 0 \\
\end{array}$

表K. ANOVA表

	平方和	\[df\]	均方	\[F\]	顯著性
迴歸	16.059	2	8.030	5.491	0.005*
殘差	317.300	217	1.462
總數	333.359	219

表L. 係數

	未標準化係數		標準化係數	t	顯著性
	B 之估計值	標準誤差	Beta 分配	t	顯著性
(常數)	5.761	0.165		34.855	0.000*
3C時間	0.011	0.039	0.018	0.271	0.787
打工時數	-0.018	0.006	-0.220	-3.313	0.001*

根據表K顯示，此迴歸模型達到顯著，再觀察表L.之迴歸係數發現打工時數係數${\beta _{\rm{1}}}$達顯著，但3C時間係數${\beta _{\rm{2}}}$未達顯著，其中打工時數標準化係數為負值，說明兩者呈顯著的負相關，也就是說打工的時數多，睡眠的時間就相對愈少。

經過多計算，發現圓夢生的睡眠除了與打工時間有關外，與性別也有關係，以打工時間與性別(虛擬變項)做為自變數，睡眠時間為應變數建立複迴歸模型如下

表M. 模型摘要

${R}$	${R^2}$	調整後的${R^2}$	Durbin-Watson
0.279	0.078	0.069	1.840

表N. ANOVA表

	平方和	\[df\]	均方	\[F\]	顯著性
迴歸	24.966	2	12.483	9.126	0.000*
殘差	295.472	216	1.368
總數	320.438	218

表O 係數

	未標準化係數		標準化係數	t	顯著性
	B 之估計值	標準誤差	Beta 分配	t	顯著性
(常數)	3.761	0.177		21.270	0.000*
性別	0.377	0.162	0.153	2.329	0.021*
打工時數	-0.176	0.054	-0.216	-3.286	0.001*

性別採虛擬變數，男生設為1，女生設為0，迴歸係數${\beta _{\rm{1}}}$達顯著，且迴歸係數為正，說明性別差異確實對於睡眠時數有影響，且女生的睡眠時數較少。

睡眠時數=3.761+0.377*性別 - 0.176*打工時數

殘差分析:(1)常態性(Normality)見下標準殘差值方圖與P-P圖

(2)獨立性(Independency):見表M之Durbin-Watson值=1.840接近2，沒有獨立性的問題。

(3)變異數同質性(Constant Variance):藉由殘差圖大致上沿著0線上下均勻跳動，符合變異數同質性的假設。

結論: 打工長短對睡眠有負面且顯著的影響，性別差異對睡眠有顯著的影響，其中女生睡眠較差，使用3C時數對睡眠時數沒有顯著影響。

雖然本校對於圓夢生的學習有實質的補助，對於打工的時數有所減少，放在學業的時間也有所改善，但補助仍只是杯水車薪的鼓勵性質，願同學在獎勵的因素下多接觸課業，對學習產生興趣提升個人的競爭力，完成大學課業後翻轉自己的人生。

--回到上面--